ML day 6: モデルの複雑さとbiasとvarianceの関係
モチベーション
モデルの過学習(Over-Fitting)と学習不足(Under-Fitting)の背後にある理論について調べたので記録しておく。
モデルの複雑さと予測誤差の関係
機械学習のモデルは複雑なほどいいというわけではないらしい。機械学習では手元にあるデータを訓練データとしてすべて突っ込むのではなく、学習用のデータと評価用データに分けるのだが、モデルが複雑すぎると学習用のデータを過学習してしまって評価用のデータでいい結果をだせないという話だそうだ。反対にシンプルすぎるモデルは学習が不十分なため期待した予測が出来ない。シンプル過ぎず、複雑すぎないモデルの構築が予測の精度を上げるらしい。
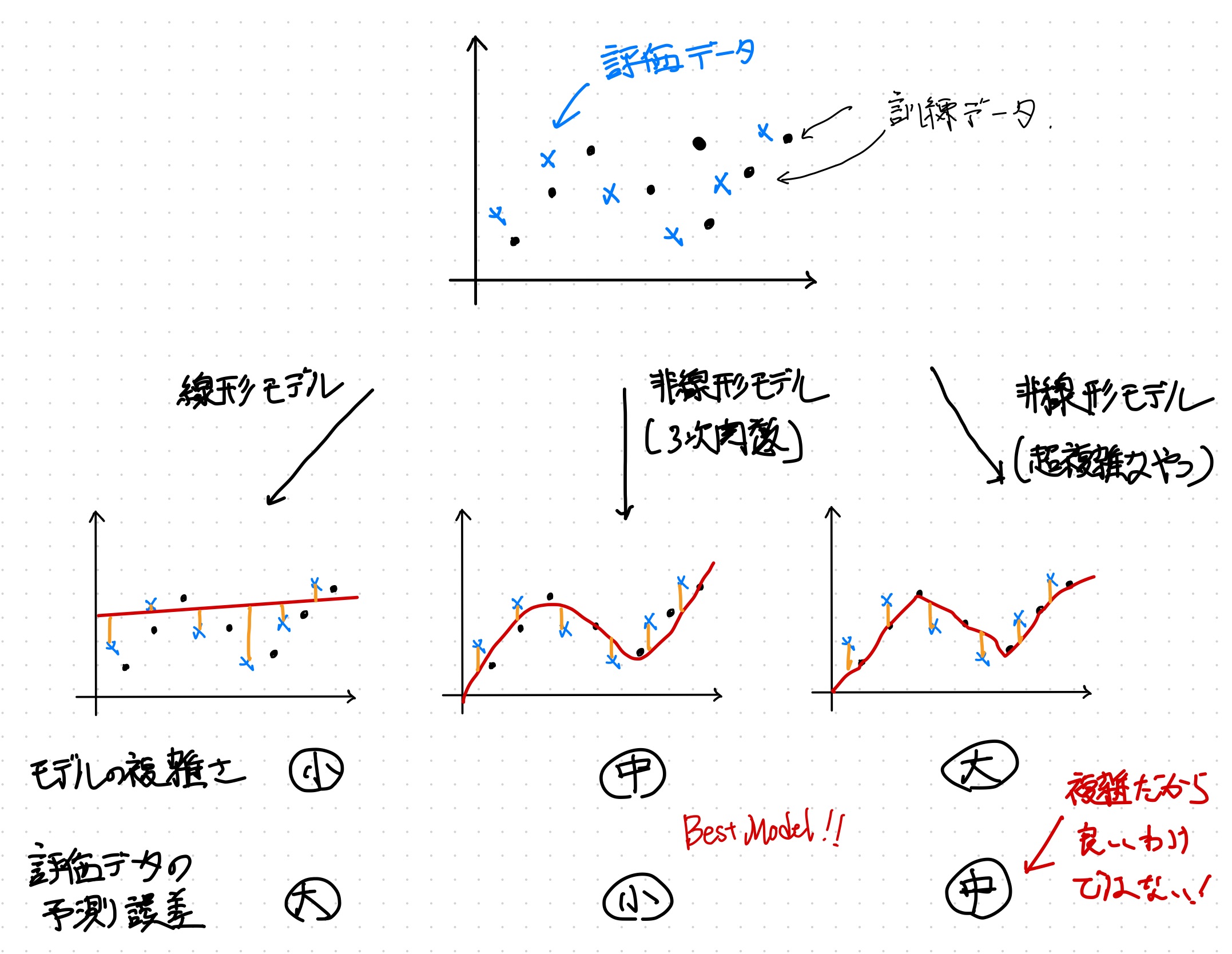
予測誤差の期待値を分解する
この話の理論的な背景を理解するには、予測誤差の二乗期待を考える必要がある。二乗しているのは実際の値と予測値の差が負にならないようにするためである。
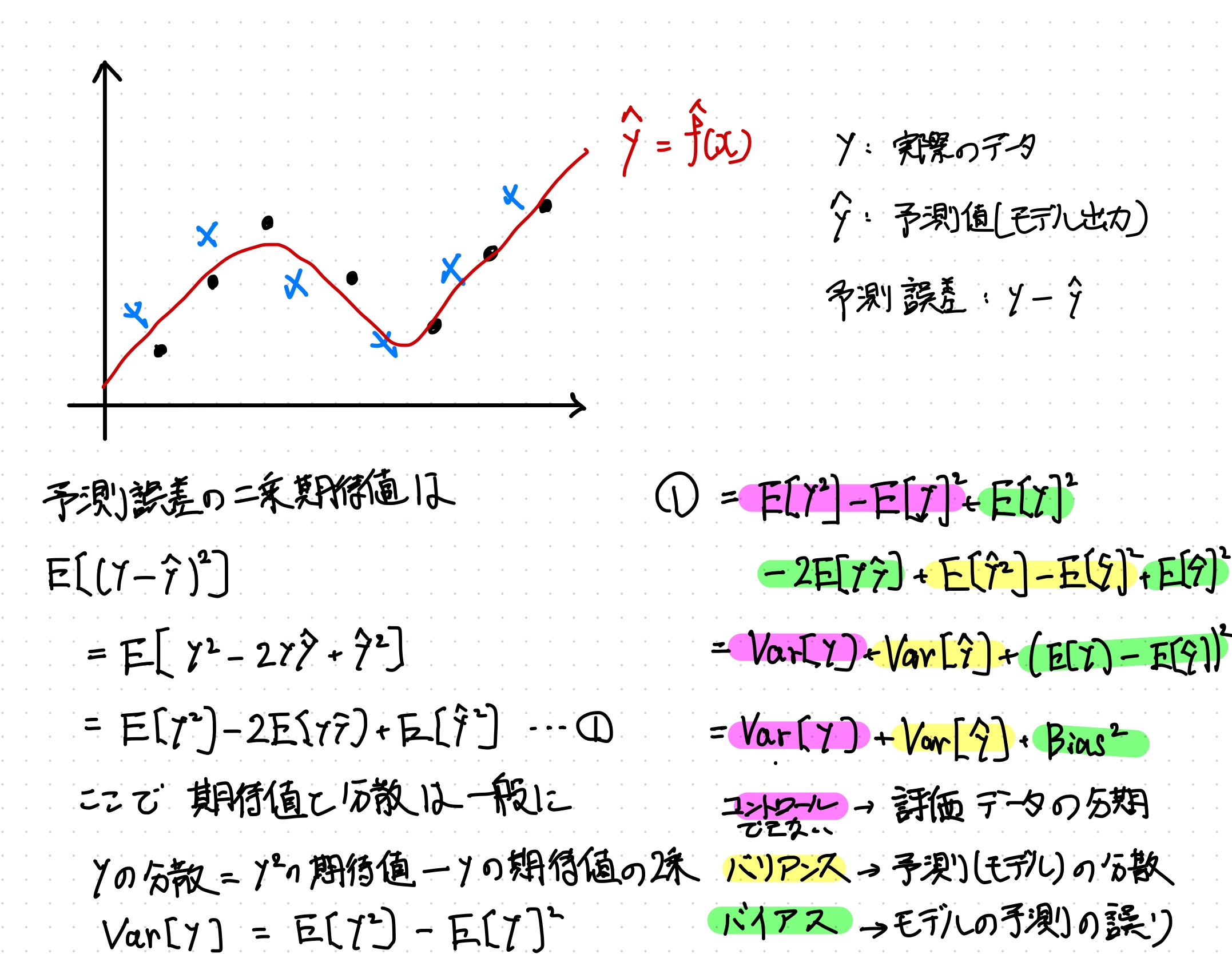
予測の誤差の期待値は最終的に評価データの分散と予測の分散とモデルの予測の誤りの和として分解できる。
$$ \begin{aligned} E[(y-\hat{y})^2] &= Var[y] + Var[\hat{y}] + (E[y] - E[\hat{y}])^2 \newline &= Var[y] + Var[\hat{y}] + Bias^2 \newline &= 訓練データの分散 + 予測値(モデル)の分散 + 予測の誤り \end{aligned} $$
この中でモデル構築者がコントロールできるのは後者の2項であり。予測の分散のことをバリアンス(Variance)といい、モデルの予測の誤りをバイアス(Bias)という。ちなみにこのVarianceとBiasだが機械学習の用語というよりは統計の基本的な考え方である。
モデルの複雑さとVariance/Biasの関係
予測誤差における Variance と Bias の関係をモデルの複雑さと共に図示したものが以下。
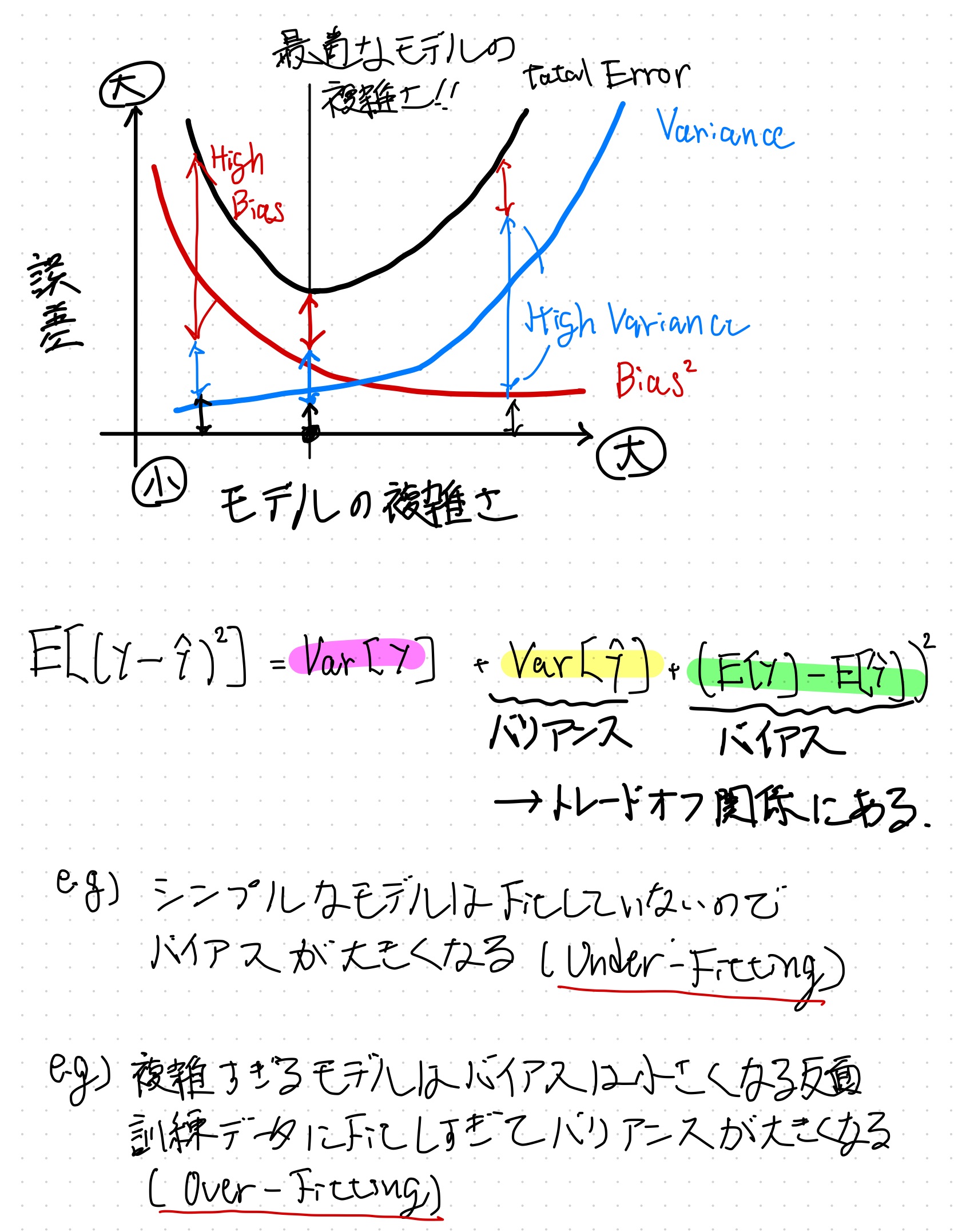
モデルがシンプル過ぎて学習できてないことを High Bias または Under-Fitting、モデルが複雑過ぎて学習データに対してFitしすぎてしまっていることを High Variance または Over-Fitting という。
所感
High Variance と High Bias どっちが Over-Fitting でどっちが Under-Fitting だっけ?と忘れそうだが、背景にある理論を理解すれば忘れることはなさそうだ。
読んでいる書籍
以下の本の”3.3 ロジスティック回帰”まで読んだ。
