ML day 7: ベクトルのノルム
モチベーション
前回はモデルの過学習(Over-Fitting)と学習不足(Under-Fitting)の背後にある理論について調べた。今回はベクトルのノルムについて調べる。これは線形回帰モデルで過学習を避けるために使われる正則化を理解するのに必要な知識である。
ベクトルのノルム
線形回帰モデルの正則化には一般的に L1, L2 ノルムが用いられる。そのためノルムとはなにかをまず理解する。Wikipedia によるとノルムは以下のように説明されている。
解析学において、ノルム (英: norm, 独: Norm) は、平面あるいは空間における幾何学的ベクトルの “長さ” の概念の一般化であり、ベクトル空間に対して「距離」を与えるための数学の道具である。ノルムの定義されたベクトル空間を線型ノルム空間または単にノルム空間という。
細かいことはわからないが、要は平面や3次元空間のべクトルの距離みたいに人間が直感的に理解できる範囲を超えた高次元ベクトル空間でも距離を扱えるように一般化しているのがノルムということだろう。機械学習においては L1 ノルムと L2 ノルムが多く用いられるようだ。
Lp ノルム
L1/L2 についている数字はどこからきたのか。これは Lp空間という関数空間の定義からきている。深く立ち入ると全く理解不能な文章を読むことになるのでサラッと理解すると、
数学の分野における Lp 空間(エルピーくうかん、英: Lp space)とは、有限次元ベクトル空間に対する p-ノルムの自然な一般化を用いることで定義される関数空間である
ということらしい。このとき、実数 p ≥ 1 に対して、x の p-ノルム(p-乗平均ノルム)あるいは Lp-ノルムは次で定義される。
この Lp-ノルムの定義においてp=1 のとき、
となり、これが L1 ノルムになる。また、 p=2 のとき
となるが、これが L2 ノルムである。 L1 ノルムはマンハッタン距離と呼ばれ、L2 ノルムはユークリッド距離と呼ばれこともある。
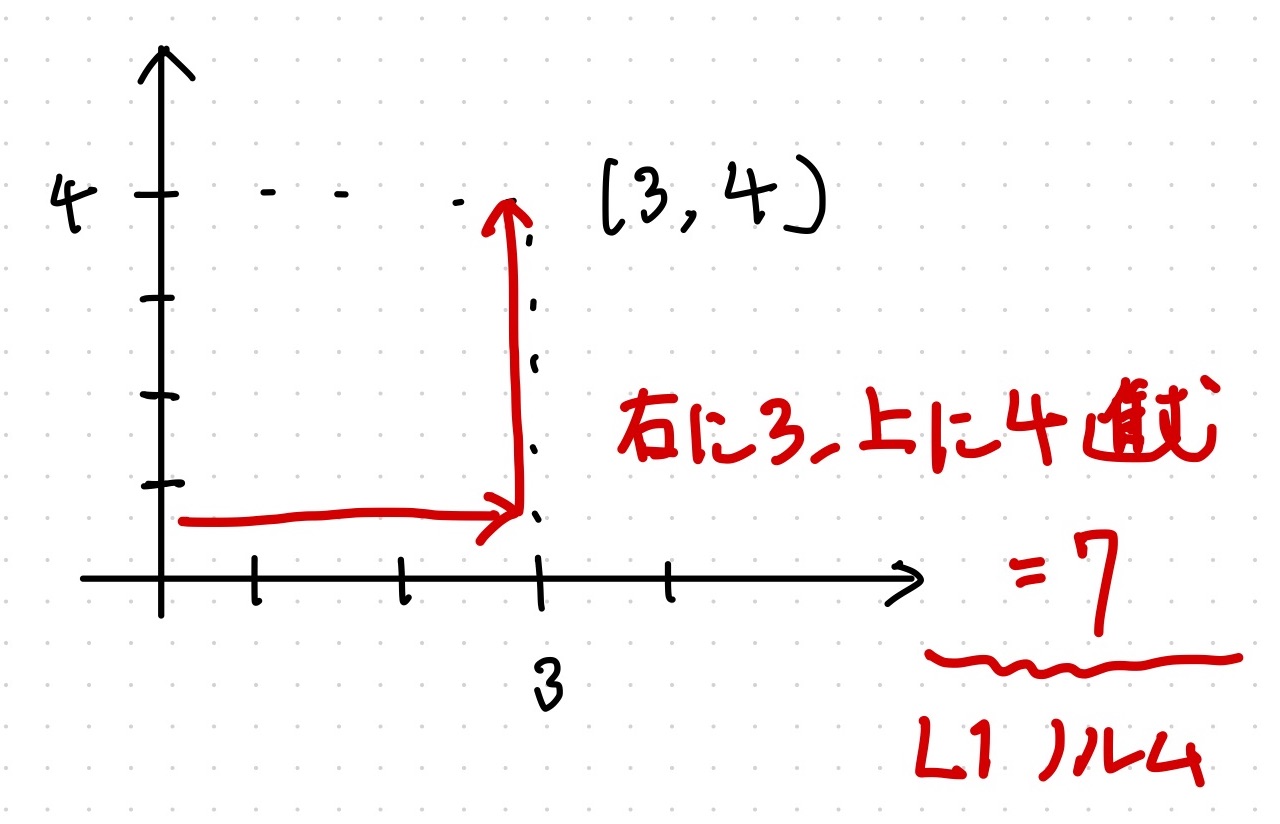
L1 ノルムのイメージ
ベクトル \(\bm{x} = (3,4)\) が与えられたとき L1 ノルムは 7 となる。
L2 ノルムのイメージ
ベクトル \(\bm{x} = (3,4)\) が与えられたとき L2 ノルムは 5 となる。
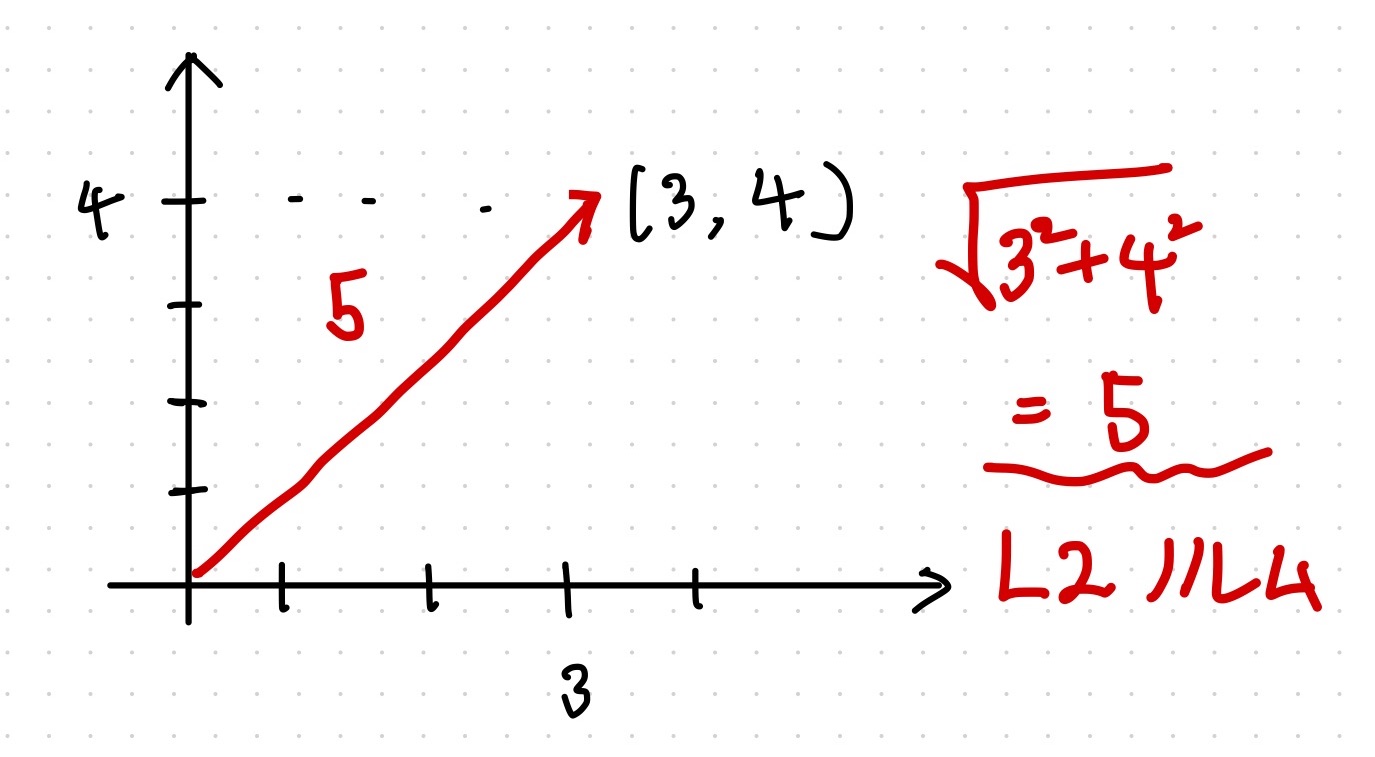
所感
そういえば、大学時代の多変量解析の講義でマンハッタン距離、ユークリッド距離を使った分類とかやったなと思いつつも、それらがどのような意味を持っているのかはすっかり忘れてしまっていた・・・
読んでいる書籍
以下の本の”3.3 ロジスティック回帰”まで読んだ。
